Матричный анализ
. Функции от матриц.
Df.
Пусть
![]() – функция скалярного аргумента. Требуется определить, что понимать под f(A), т.е. нужно распространить функцию f(x) на матричное значение аргумента.
– функция скалярного аргумента. Требуется определить, что понимать под f(A), т.е. нужно распространить функцию f(x) на матричное значение аргумента.
Решение этой задачи известно, когда f(x) – многочлен:
![]() , тогда
, тогда
![]() .
.
Определение f(A) в общем случае.
Пусть m(x) – минимальный многочлен А и он имеет такое каноническое разложение
![]() ,
,
![]() ,
,
![]() – собственные значения А. Пусть многочлены g(x) и h(x) принимают одинаковые значения.
– собственные значения А. Пусть многочлены g(x) и h(x) принимают одинаковые значения.
Пусть g(A)=h(A) (1), тогда многочлен d(x)=g(x)-h(x) – аннулирующий многочлен для А, так как d(A)=0, следовательно, d(x) делится на линейный многочлен, т.е. d(x)=m(x)*q(x) (2).
Тогда
![]() , т.е.
, т.е.
![]() (3),
(3),
![]() ,
,
![]() ,
,
![]() .
.
Условимся m чисел для f(x) таких
![]() называть значениями функции f(x) на спектре матрицы А, а множество этих значений будем обозначать
называть значениями функции f(x) на спектре матрицы А, а множество этих значений будем обозначать
![]() .
.
Если множество f(Sp A) определено для f(x), то функция определена на спектре матрицы А.
Из (3) следует, что многочлены h(x) и g(x) имеют одинаковые значения на спектре матрицы А.
Наши рассуждения обратимы, т.е. из (3) Ю (3) Ю (1). Таким образом, если задана матрица А, то значение многочлена f(x) вполне определяется значениями этого многочлена на спектре матрицы А, т.е. все многочлены g i (x), принимающие одинаковые значения на спектре матрицы имеют одинаковые матричные значения g i (A). Потребуем, чтобы определение значения f(A) в общем случае подчинялось такому же принципу.
Значения функции f(x) на спектре матрицы А должны полносильно определить f(A), т.е. функции, имеющие одни и те же значения на спектре должны иметь одно и то же матричное значение f(A). Очевидно, что для определения f(A) в общем случае, достаточно найти многочлен g(x), который бы принимал те же значения на спектре А, что и функция f(A)=g(A).
Df.
Если f(x) определена на спектре матрицы А, то f(A)=g(A), где g(A) – многочлен, принимающий на спектре те же значения, что и f(A),Df.
Значением функции от матрицы А назовем значение многочлена от этой матрицы приСреди многочленов из С[x], принимающих одинаковые значения на спектре матрицы А, что и f(x), степени не выше (m-1), принимающий одинаковые значения на спектре А, что и f(x) – это остаток от деления любого многочлена g(x), имеющего те же значения на спектре матрицы А, что и f(x), на минимальный многочлен m(x)=g(x)=m(x)*g(x)+r(x).
Этот многочлен r(x) называют интерполяционным многочленом Лагранжа-Сильвестра для функции f(x) на спектре матрицы А.
Замечание.
Если минимальный многочлен m(x) матрицы А не имеет кратных корней, т.е.
![]() , то значение функции на спектре
, то значение функции на спектре
![]() .
.
Пример:
Найти r(x) для произвольной f(x), если матрица
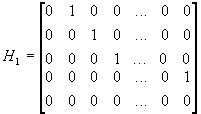 . Построим f(H
1
). Найдем минимальный многочлен H
1
– последний инвариантный множитель [xE-H
1
]:
. Построим f(H
1
). Найдем минимальный многочлен H
1
– последний инвариантный множитель [xE-H
1
]:
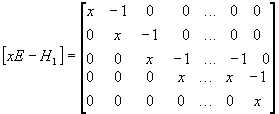 , d
n-1
=x
2
; d
n-1
=1;
, d
n-1
=x
2
; d
n-1
=1;
m x =f n (x)=d n (x)/d n-1 (x)=x n Ю 0 – n –кратный корень m(x), т.е. n-кратные собственные значения H 1 .
![]() , r(0)=f(0), r’(0)=f’(0),…,r
(n-1)
(0)=f
(n-1)
(0)
Ю
, r(0)=f(0), r’(0)=f’(0),…,r
(n-1)
(0)=f
(n-1)
(0)
Ю
![]() .
.
Свойство № 1.
Доказательство:
Пусть характеристический многочлен матрицы А имеет вид:
![]() ,
,
![]() ,
,
![]() . Посчитаем
. Посчитаем
![]() . Перейдем от равенства к определителям:
. Перейдем от равенства к определителям:
![]()
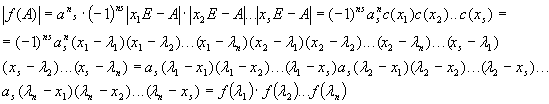
Сделаем замену в равенстве:
![]() (*)
(*)
Равенство (*) справедливо для любого множества f(x), поэтому заменим многочлен f(x) на
![]() , получим:
, получим:
![]() .
.
Слева мы получили характеристический многочлен для матрицы f(A), разложенный справа на линейные множители, откуда следует, что
![]() – собственные значения матрицы f(A).
– собственные значения матрицы f(A).
ЧТД.
Свойство № 2.
Пусть матрица
![]() и
и
![]() – собственные значения матрицы А, f(x) – произвольная функция, определенная на спектре матрицы А, тогда собственные значения матрицы f(A) равны
– собственные значения матрицы А, f(x) – произвольная функция, определенная на спектре матрицы А, тогда собственные значения матрицы f(A) равны
![]() .
.
Доказательство:
Т.к. функция f(x) определена на спектре матрицы А, то существует интерполяционный многочлен матрицы r(x) такой, что
![]() , а тогда f(A)=r(A), а у матрицы r(A) собственными значениями по свойству № 1 будут
, а тогда f(A)=r(A), а у матрицы r(A) собственными значениями по свойству № 1 будут
![]() которым соответственно равны
которым соответственно равны
![]() .
.
ЧТД.
Свойство № 3.
Если А и В подобные матрицы,
![]() , т.е.
, т.е.
![]() , и f(x) – произвольная функция, определенная на спектре матрицы А, тогда
, и f(x) – произвольная функция, определенная на спектре матрицы А, тогда
![]()
Доказательство:
Т.к. А и В подобны, то их характеристические многочлены одинаковы
Ю
одинаковы и их собственные значения, поэтому значение f(x) на спектре матрицы А совпадает со значение функции f(x) на спектре матрицы В, при чем существует интерполяционный многочлен r(x) такой, что f(A)=r(A),
![]() ,
,
![]() Ю
Ю
![]() .
.
ЧТД.
Свойство № 4.
Если А – блочно-диагональная матрица
![]() , то
, то
![]()
Следствие:
Если
![]() , то
, то
![]() , где f(x) – функция, определенная на спектре матрицы А.
, где f(x) – функция, определенная на спектре матрицы А.
- Интерполяционный многочлен Лагранжа-Сильвестра.
Случай № 1.
Пусть дана
![]() . Рассмотрим первый случай: характеристический многочлен
. Рассмотрим первый случай: характеристический многочлен
![]() имеет ровно n корней, среди которых нет кратных, т.е. все собственные значения матрицы А различны, т.е.
имеет ровно n корней, среди которых нет кратных, т.е. все собственные значения матрицы А различны, т.е.
![]() , Sp A – простой. В этом случае построим базисные многочлены l
k
(x):
, Sp A – простой. В этом случае построим базисные многочлены l
k
(x):
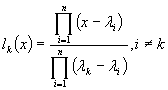 .
.
Пусть f(x) – функция, определенная на спектре матрицы А и значениями этой функции на спектре будут
![]() . Надо построить
. Надо построить
![]() .
.
Построим:
![]() .
.
Обратим внимание, что
![]() .
.
![]()
![]()
Пример: Построить интерполяционный многочлен Лагранжа-Сильвестра для матрицы
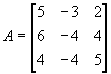 .
.
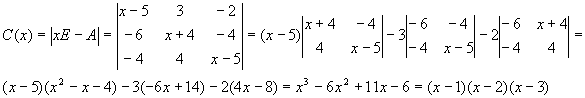 Построим базисные многочлены:
Построим базисные многочлены:
![]()
![]()
![]()
Тогда для функции f(x), определенной на спектре матрицы А, мы получим:
![]() .
.
Возьмем
![]() , тогда интерполяционный многочлен
, тогда интерполяционный многочлен
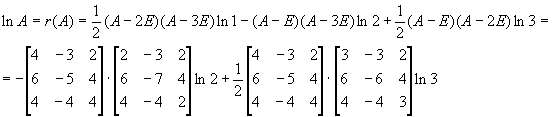 .
.
Случай № 2.
Характеристический многочлен матрицы А имеет кратные корни, но минимальный многочлен этой матрицы является делителем характеристического многочлена и имеет только простые корни, т.е.
![]() . В этом случае интерполяционный многочлен строится так же как и в предыдущем случае.
. В этом случае интерполяционный многочлен строится так же как и в предыдущем случае.
Случай № 3.
Рассмотрим общий случай. Пусть минимальный многочлен имеет вид:
![]() ,
,
где m 1 +m 2 +…+m s =m, deg r(x)<m.
Составим дробно-рациональную функцию:
![]() и разложим ее на простейшие дроби.
и разложим ее на простейшие дроби.
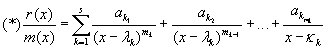
Обозначим:
![]() . Умножим (*) на
. Умножим (*) на
![]() и получим
и получим
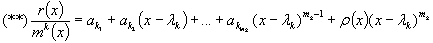
где
![]() – некоторая функция, не обращающаяся в бесконечность при
– некоторая функция, не обращающаяся в бесконечность при
![]() .
.
Если в (**) положить
![]() , получим:
, получим:
![]()
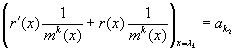
Для того, чтобы найти a k3 надо (**) продифференцировать дважды и т.д. Таким образом, коэффициент a ki определяется однозначно.
После нахождения всех коэффициентов вернемся к (*), умножим на m(x) и получим интерполяционный многочлен r(x), т.е.
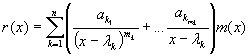 .
.
Пример: Найти f(A), если
![]() , где t – некоторый параметр,
, где t – некоторый параметр,
![]() .
.
Найдем минимальный многочлен матрицы А:
![]()
![]()
![]() .
.
Проверим, определена ли функция на спектре матрицы А
![]()
![]()
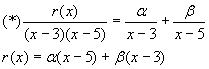
Умножим (*) на (х-3)
![]()
при х=3
![]() Ю
Ю
![]()
Умножим (*) на (х-5)
![]()
![]() .
.
Таким образом,
![]() - интерполяционный многочлен.
- интерполяционный многочлен.
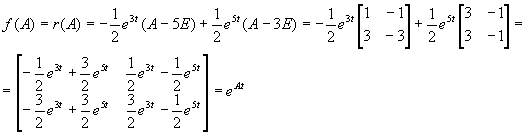
Пример 2.
Если
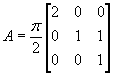 , то доказать, что
, то доказать, что
![]()
Найдем минимальный многочлен матрицы А:
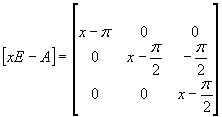 - характеристический многочлен.
- характеристический многочлен.
![]()
![]()
![]()
d 2 (x)=1, тогда минимальный многочлен
![]()
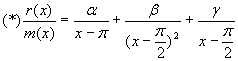 .
.
Рассмотрим f(x)=sin x на спектре матрицы:
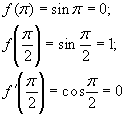 Ю
функция является определенной на спектре.
Ю
функция является определенной на спектре.
Умножим (*) на
![]()
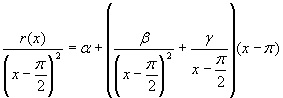 Ю
Ю
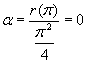 .
.
Умножим (*) на
![]() :
:
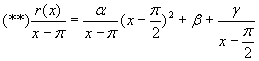
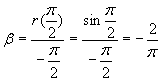 .
.
Вычислим g , взяв производную (**):
![]() . Полагая
. Полагая
![]() ,
,
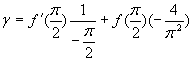 , т.е.
, т.е.
![]() .
.
Итак,
![]() ,
,
![]() ,
,
![]() ,
,
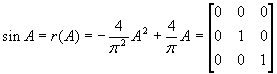 .
.
ЧТД.
Пример 3.
Пусть f(x) определена на спектре матрицы, минимальный многочлен которой имеет вид
![]() . Найти интерполяционный многочлен r(x) для функции f(x).
. Найти интерполяционный многочлен r(x) для функции f(x).
Решение: По условию f(x) определена на спектре матрицы А Ю f(1), f’(1), f(2), f ‘(2), f ‘’ (2) определены.
![]() .
.
![]()
![]()
![]() .
.
Используем метод неопределенных коэффициентов:
![]()
![]()
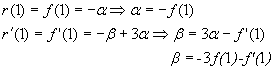
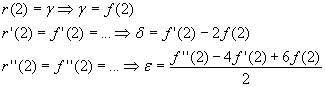
Если f(x)=ln x
f(1)=0 f’(1)=1
f(2)=ln 2 f’(2)=0.5 f’’(2)=-0.25
4. Простые матрицы.
Пусть матрица
![]() , так как С алгебраически замкнутое поле, то характеристический многочлен
, так как С алгебраически замкнутое поле, то характеристический многочлен
![]() , где
, где
![]() , k
i
– алгебраическая кратность корня
, k
i
– алгебраическая кратность корня
![]() .
.
Обозначим множество векторов удовлетворяющих собственному значению
![]()
![]() - подпространство,
- подпространство,
![]() , где r – ранг матрицы
, где r – ранг матрицы
![]() .
.
Теорема.
Если квадратная матрица А имеет собственное значение
![]() , а матрица
, а матрица
![]() имеет
имеет
![]() , то
, то
![]() имеет кратность
имеет кратность
![]() .
.
DF
. Размерность
![]() называется геометрической кратностью собственного значения
называется геометрической кратностью собственного значения
![]() .
.
В свете этого определения теорема переформулируется следующим образом:
Теорема. Алгебраическая кратность собственного значения не меньше его геометрической кратности.
DF
. Матрица
![]() называется простой, если аглебраическая кратность каждого ее собственного значения совпадает с его геометрической кратностью.
называется простой, если аглебраическая кратность каждого ее собственного значения совпадает с его геометрической кратностью.
Из линейной алгебры следует, что матрица
![]() простая тогда и только тогда, когда
простая тогда и только тогда, когда
![]() .
.
Если матрица А простая, тогда существует n линейно независимых собственных векторов x
1
, x
2
, …,x
n
таких, что
![]() , для
, для
![]() . Запишем это равенство в матричном виде:
. Запишем это равенство в матричном виде:
![]()
![]() , т.е. А – простая тогда и только тогда, когда
, т.е. А – простая тогда и только тогда, когда
![]() и
и
![]() .
.
Замечание.
Обратим внимание на то, что собственные значения А и А’ совпадают. Действительно, собственные значения для А’ это значения
![]() . Таким образом характеристические многочлены матриц совпадают. Размерность
. Таким образом характеристические многочлены матриц совпадают. Размерность
![]() , тогда
, тогда
![]() . Поэтому, если
. Поэтому, если
![]() - собственное значение матрицы А, то и
- собственное значение матрицы А, то и
![]() является собственным значением матрицы А’, т.е. существует
является собственным значением матрицы А’, т.е. существует
![]() , что
, что
![]() (*) или
(*) или
![]() . Транспонируем (*) и получим
. Транспонируем (*) и получим
![]() (транспонируем это равенство). В этом случае
(транспонируем это равенство). В этом случае
![]() называют левым собственным вектором матрицы А. Соответственно,
называют левым собственным вектором матрицы А. Соответственно,
![]() - называют правым собственным подпространством,
- называют правым собственным подпространством,
![]() - называют левым собственным подпространством.
- называют левым собственным подпространством.
Рассмотрим следующую конструкцию: если матрица А простая, то существует n линейно независимых собственных векторов x
1
, x
2
, …, x
n
и существует n линейно независимых собственных векторов y
1
, y
2
,…,y
n
, где x
1
, x
2
, …, x
n
такие, что
![]() ,
,
![]() (1); y
1
, y
2
,…,y
n
такие, что
(1); y
1
, y
2
,…,y
n
такие, что
![]() (2),
(2),
![]() .
.
Запишем равенство (1) в виде
![]() (3)
Ю
что, если А – простая, то существуют матрицы X и Y, что
(3)
Ю
что, если А – простая, то существуют матрицы X и Y, что
![]() или
или
![]() (**).
(**).
DF
. Множества векторов x
1
, x
2
, …, x
n
и y
1
, y
2
,…,y
n
удовлетворяющие условию
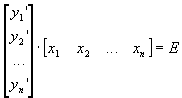 , т.е.
, т.е.
![]() называются
квазиортогональными
.
называются
квазиортогональными
.
Учитывая равенство (**) и определение делаем вывод: множества левых и правых собственных векторов простой матрицы А квазиортогональны и
![]() .
.
Очень важной для матриц является следующая теорема:
СПЕКТРАЛЬНАЯ ТЕОРЕМА.
Если А – простая матрица порядка n над полем С и p(x) многочлен из кольца C[x], и x
1
, x
2
, …, x
n
и y
1
, y
2
,…,y
n
– множества правых и левых собственных векторов матрицы А, то
![]() , а сопутствующая матрица
, а сопутствующая матрица
![]() , где
, где
![]() .
.
Следствие . Сопутствующие матрицы обладают следующими свойства:
Пример. Показать, что матрица
![]() простая. Найти сопутствующие матрицы для матрицы А и использовать их для А
20
, p(x)=x
20
.
простая. Найти сопутствующие матрицы для матрицы А и использовать их для А
20
, p(x)=x
20
.
Решение:
![]()
![]()
![]() Ю
Ю
существуют 2 линейно независимые правые и левые системы собственных векторов.
Найдем правые собственные векторы:
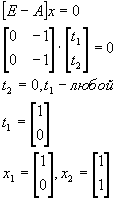
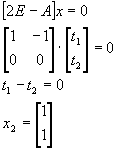
Найдем левые собственные векторы:
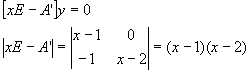
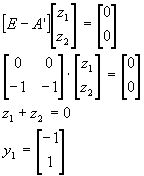
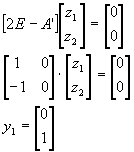
Найдем сопутствующие матрицы:
![]()
![]()
![]() .
.
5.Спектральное разложение функции f(A).
Спектральное разложение для f(A) имеет важное значение и очевидно тесно примыкает к спектральной теореме для простых матриц.
Пусть дана матрица
![]() и пусть
и пусть
![]() ,
,
![]() .
.
Теорема.
Если
![]() , а функция f(x) определена на спектре матрицы А и
, а функция f(x) определена на спектре матрицы А и
![]() - значение j-й производной от f(x) в собственном значении
- значение j-й производной от f(x) в собственном значении
![]() , где
, где
![]() ,
,
![]() , то существуют такие независимые от f(x) матрицы
, то существуют такие независимые от f(x) матрицы
![]() , что (1)
, что (1)
![]() , при чем
, при чем
![]() коммутирует с матрицей А и образуют линейно независимую систему в пространстве
коммутирует с матрицей А и образуют линейно независимую систему в пространстве
![]()
Доказательство:
заметим, что
![]() и
и
![]() , где
, где
![]() - базисные многочлены, принимающие одинаковые значения на спектре матрицы А,
- базисные многочлены, принимающие одинаковые значения на спектре матрицы А,
![]() (3). Сравнивая (1) и (2) и учитывая (3) получим, что
(3). Сравнивая (1) и (2) и учитывая (3) получим, что
![]() . Матрицы
. Матрицы
![]() называются компонентами матрицы А или компонентными матрицами.
называются компонентами матрицы А или компонентными матрицами.
ЧТД.
Опишем следующие свойств компонентных матриц, которые в некоторой степени обобщают свойства сопровождающих матриц.
Теорема
. Компонентные матрицы
![]() обладают следующими свойствами:
обладают следующими свойствами:
.
Замечание. Для того, чтобы найти компонентные матрицы для f(x) определенной на спектре матрицы А необходимо и достаточно знать базисные многочлены, входящие в интерполяционный многочлен, однако нахождение интерполяционного многочлена f(x) связано с некоторыми трудностями, а поэтому будем вычислять компонентные матрицы подбирая соответствующим образом системы функций.
Пример: Найти компоненты для матрицы
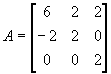 .
.
![]() .
.
Пусть f(x) определена на спектре А, тогда согласно спектральной теореме
![]() .
.
- f(x)=1
- f(x)=x-4
- f(x)=(x-4) 2
E=1Z 11 +0Z 12 +1Z 21 =Z 11 +Z 21
A-4E=0Z 11 +1Z 12+ (-2 ) Z 21 =Z 12 -2Z 21
(A-4E) 2 =4Z 21
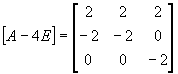
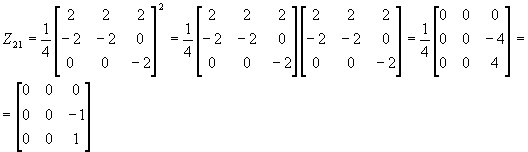
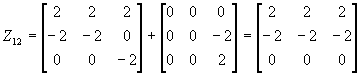
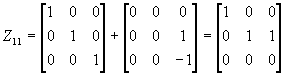 .
.
Таким образом, для любой функции f(x), определенное на спектре матрицы А
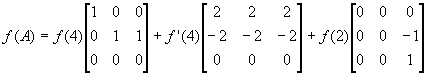
![]()
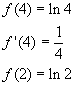
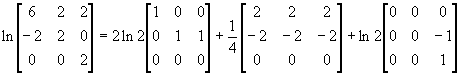
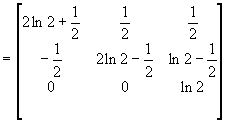 .
.
Пример 2.
Найти компоненты для матрицы
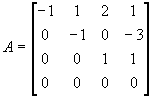 .
.
Найдем минимальный многочлен матрицы А.
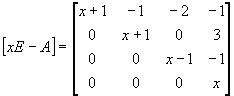
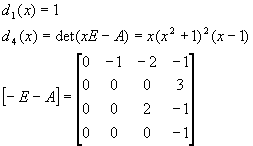
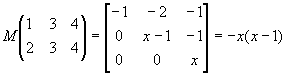
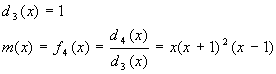
![]()
![]()
- f(x)=1
- f(x)=x+1
- f(x)=(x+1) 2
- f(x)=x-1
E=Z 11 +Z 21 +Z 31
(A+E)=2Z 21 +Z 31 +Z 12
(A+E) 2 =4Z 21 +Z 31
A-E=-2Z 11 +Z 12 -Z 31
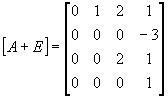
![]()
1. f(x)=1 E=Z 11 +Z 21 +Z 31
2. f(x)=x+1 A+E=Z 11 Z 22 +2Z 31
3. f(x)=(x+1) 2 (A+E) 2 =Z 11 +4Z 31
4. f(x)=x-1 (A-E)=-Z 11 -2Z 21 +Z 22
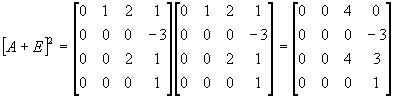
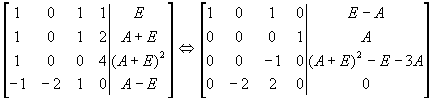
Z 31 =A
-Z 22 =(A+E) 2 -E-3A
Z 12 =Z 22
Z 11 =(E-A)-Z 22
6.Определенные матрицы.
Эрмитовы и квадратичные матрицы.
Пусть А – эрмитова матрица (А * =А).
Рассмотрим функцию h(x) – действительная функция комплексного аргумента.
Рассмотрим:
![]()
DF
. Функция
![]() , где А – эрмитова матрица, называется эрмитовой формой от n переменных x
1
, …, x
n
, где А – матрица эрмитовой формы.
, где А – эрмитова матрица, называется эрмитовой формой от n переменных x
1
, …, x
n
, где А – матрица эрмитовой формы.
Очевидно, что если А – действительная симметрическая матрица, то в этом случае получаем квадратичную форму
![]() .
.
Для каждой эрмитовой (квадратичной) формы инвариантами являются: ранг (число не нулевых коэффициентов в квадратичной форме нормального вида совпадающих с рангом матрицы А), p (индекс) – число положительных коэффициентов в квадратичной форме нормального вида, оно совпадает с числом положительных собственных значений, сигнатура . Эти числа r, p, гр-r не зависят от тех преобразований, которые совершаются над данными формами.
В дальнейшем ограничимся рассмотрением только квадратичных форм. Нас интересуют 2 семейства матриц.
DF
. Действительная симметрическая матрица А называется
положительно определенной
, если
![]() для
для
![]() .
.
DF
. Действительная симметрическая матрица А называется
неотрицательно определенной
, если
![]() для
для
![]() .
.
Оба типа матриц относятся к классу определенных матриц. Заметим, что положительно определенная матрица невырожденная, т.е. если предположить, что она вырожденная, то
![]() ,
,
![]() , что противоречит условию.
, что противоречит условию.
Теорема № 1.
Действительная симметрическая матрица n-го порядка будет определенной ранга
![]() тогда и только тогда , когда она имеет r положительных собственных значений, а остальные (n-r) – собственные значения равны 0.
тогда и только тогда , когда она имеет r положительных собственных значений, а остальные (n-r) – собственные значения равны 0.
Теорема № 2. Действительная симметрическая матрица положительна определена тогда и только тогда, когда все ее главные миноры положительны.
Теорема № 3 . Действительная симметрическая матрица положительно определена тогда и только тогда, когда все ее главные миноры положительны.
7.Неотрицательные матрицы.
DF
. Матрица
![]() называется
неотрицательной,
если каждый ее элемент положителен.
называется
неотрицательной,
если каждый ее элемент положителен.
Квадратные матрицы такого типа возникают во множестве задач и это определяющее свойство приводит к сильным результатам об их строении. Теорема Фробениуса-Перона является основным результатом для неотрицательных матриц.
Пусть матрицы
![]() . Будем говорить, что
. Будем говорить, что
![]() , если
, если
![]() б в частности A>B, если
б в частности A>B, если
![]() .
.
Вспомним матрицу перестановки
![]() , т.е. матрицы перестановки обязательно ортогональны. Произведение
, т.е. матрицы перестановки обязательно ортогональны. Произведение
![]() приводит к перестановке столбцов матрицы А.
приводит к перестановке столбцов матрицы А.
DF
. При
![]() матрица
матрица
![]() называется
приводимой матрицей
, если существует такая матрица перестановки Р, что
называется
приводимой матрицей
, если существует такая матрица перестановки Р, что
![]() совподает с матрицей
совподает с матрицей
![]() , где А
11
, А
12
, А
22
– квадратные матрицы меньшего чем n порядка. Если матрица Р не существует, то матрица А называется
неприводимой
.
, где А
11
, А
12
, А
22
– квадратные матрицы меньшего чем n порядка. Если матрица Р не существует, то матрица А называется
неприводимой
.
Понятие приводимости имеет значение при решении матричных уравнений
![]() , ибо если Ф – приводима, то осуществив замену переменных, которую подсказывают равенства
, ибо если Ф – приводима, то осуществив замену переменных, которую подсказывают равенства
![]() , получаем
, получаем
![]() , где
, где
![]() ,
,
![]() .
.
![]() и решаем матричное уравнение с матрицей более низкого порядка. Затем,
и решаем матричное уравнение с матрицей более низкого порядка. Затем,
![]() и решаем матричное уравнение. Таким образом, если А – приводима, то решение уравнения высокого порядка сводится к решению уравнений более низкого порядка, при чем собственные значения матриц А
11
и А
22
в своей совокупности составляет множество значений матрицы А.
и решаем матричное уравнение. Таким образом, если А – приводима, то решение уравнения высокого порядка сводится к решению уравнений более низкого порядка, при чем собственные значения матриц А
11
и А
22
в своей совокупности составляет множество значений матрицы А.
Интересно, что явление приводимости не связано с величиной матрицы, а зависит лишь от расположения нулевых элементов в матрице.
В связи с этим, используют идею направленного графа матрицы, которую можно взять в качестве характеризации неприводимости матрицы. Наметим первые шаги тоерии и получим вторую характеризацию неприводимости матриц.
DF
. Пусть р
1
, р
2
, …, р
n
– n различных точек комплексной плоскости и
![]() . Для каждого нулевого элемента матрицы А
. Для каждого нулевого элемента матрицы А
![]() составим направленную линию от р
i
к р
j
составим направленную линию от р
i
к р
j
![]() . Получающаяся в результате фигура на комплексной плоскости называется
направленным графом матрицы
.
. Получающаяся в результате фигура на комплексной плоскости называется
направленным графом матрицы
.
Например:
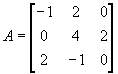
DF
. Говорят, что любой направленный граф связен, если для каждой пары точек
![]() существует направленный путь
существует направленный путь
![]() .
.
Легко доказать, что квадратная матрица неприводима тогда и только тогда, когда ее граф является связным.
8.Теорема Фробениуса-Перона.
Очевидно, что если
![]() , то для
, то для
![]()
![]() . Более того, мы покажем, что для достаточно больших p
. Более того, мы покажем, что для достаточно больших p
![]() .
.
Лемма № 1.
Если матрица
![]() неотрицательна и неприводима, то
неотрицательна и неприводима, то
![]() .
.
Доказательство:
Если взять произвольный вектор
![]() и
и
![]() , то
, то
![]() . И пусть вектор
. И пусть вектор
![]() имеет место, очевидно, что Z имеет по крайней мере столько же нулевых положительных элементов, что и y. В самом деле, если предположить, что Z имеет меньше нулевых компонент, то обозначим
имеет место, очевидно, что Z имеет по крайней мере столько же нулевых положительных элементов, что и y. В самом деле, если предположить, что Z имеет меньше нулевых компонент, то обозначим
![]() , тогда
, тогда
![]() и разбив матрицу А на блоки следующим образом
и разбив матрицу А на блоки следующим образом
![]() мы будем иметь
мы будем иметь
![]() .
.
Учитывая, что
![]() , то
, то
![]() , тогда получаем, что
, тогда получаем, что
![]() , что противоречит неприводимости матрицы.
, что противоречит неприводимости матрицы.
Для следующего вектора повторим рассуждения и т.д. В итоге получим, что для некоторого ненулевого вектора y
![]() .
.
ЧТД.
Для ненулевой неприводимой матрицы А рассмотрим действительную функцию r(x), определенную для ненулевых векторов
![]() следующим образом:
следующим образом:
![]() , (Ax)
i
– i-я координата вектора Ах.
, (Ax)
i
– i-я координата вектора Ах.
![]() . Из определения следует, что
. Из определения следует, что
![]() и кроме того, r(x) –такое наименьшее значение
и кроме того, r(x) –такое наименьшее значение
![]() , что
, что
![]() .
.
Очевидно, что r(x) инвариантна относительна замены x на
![]() , поэтому в дальнейшем можно рассматривать замкнутое множество
, поэтому в дальнейшем можно рассматривать замкнутое множество
![]() , такое
, такое
![]() .
.
Однако, r(x) может иметь разрывы в точках, где координата x обращается в 0, поэтому рассмотрим множество векторов
![]() и обозначим
и обозначим
![]() . По лемме № 1 каждый вектор из N будет положительным, а поэтому
. По лемме № 1 каждый вектор из N будет положительным, а поэтому
![]() т.е.
т.е.
![]() для
для
![]() .
.
Обозначим через
![]() наибольшее число, для которого
наибольшее число, для которого
![]() ,
,
![]() .
.
![]() –
спектральный радиус матрицы А
. Если
–
спектральный радиус матрицы А
. Если
![]() Можно показать, что существует вектор y, что
Можно показать, что существует вектор y, что
![]() .
.
Замечание. Могут существовать и другие векторы в L для которых r(x) принимает значение r, поэтому любой такой вектор называется экстремальным для матрицы А (Az=rz).
Интерес к числу r объясняется следующим результатом.
Лемма № 2.
Если матрица
![]() неотрицательна и неприводима, то число
неотрицательна и неприводима, то число
![]()
![]() является собственным значением матрицы А, кроме того каждый экстремальный вектор для А положителен и является правым собственным вектором для А, отвечающим собственному значению r.
является собственным значением матрицы А, кроме того каждый экстремальный вектор для А положителен и является правым собственным вектором для А, отвечающим собственному значению r.
Основным результатом является теорема Фробениуса-Перона для непрерывных матриц.
Теорема Фробениуса-Перона
. Если матрица
![]() неотрицательна и неприводима, то:
неотрицательна и неприводима, то:
- А имеет положительное собственное значение, равное спектральному радиусу матрицы А;
- существует положительный правый собственный вектор, соответствующий собственному значению r.
- собственное значение имеет алгебраическую кратность равную 1.
Эта теорема была опубликована в 1912 году Фробениусом и явилась обобщением теоремы Перона, которая является следствием.
Теорме Перона (следствие). Положительная квадратная матрица А имеет положительное и действительное собственное значение r, имеющее алгебраическую кратность 1 и превосходит модули всех других собственных значений матрицы А. Этому r соответствует положительный собственный вектор.
Используя теорему Фробениуса-Перона, можно найти максимальное действительное значение матрицы, не используя характеристического многочлена матрицы.
 При любом использовании материалов установите обратную ссылку на своем сайте.
При любом использовании материалов установите обратную ссылку на своем сайте.
