|
| ИЗГИБ С КРУЧЕНИЕМ КРУГЛЫХ ВАЛОВ |
| |
| |
| Для использования основных расчетных формул, использующих
эквивалентные напряжения, необходимо определить главные нормальные напряжения.
(Три главные напряжения определяются кубическим уравнением, точные решения
которого даются формулами Кордано). |
 |
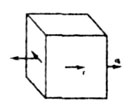| Рис. 7.3 |
| Однако в частном, но часто встречающемся случае плоского
напряженного состояния, когда имеется совместное кручение и изгиб (или растяжение),
возникает напряженное состояние, показанное на рис. 7.3 |
| В этом случае максимальное и минимальное напряжения определяются
формулой: |
 |
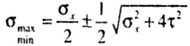Следовательно, учитывая, что  ,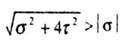
главные нормальные напряжения будут следующими: |
 |
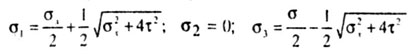| при этом эквивалентные напряжения примут вид: по теории наибольших
касательных напряжений (3-я теория) |
 |
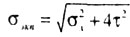| по энергетической теории (4-я теория) |
 |
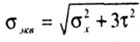| по теории Мора (5-я теория) |
 |
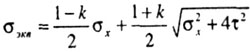Сравнивая выражения для эквивалентных напряжений по теории
наибольших касательных напряжений и энергетической теории, при  >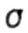
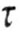 , что и имеет место в большинстве
случаев, обе теории дают близкие друг к другу результаты. |
| Для стержней круглого поперечного сечения, для которых момент
сопротивления кручению Wk
в два раза больше момента сопротивления изгибу Wизг:
Wk
= 2W, при воздействии на них изгибающего М и крутящего Мk
моментов, последние три формулы принимают соответствующивй вид: |
 |
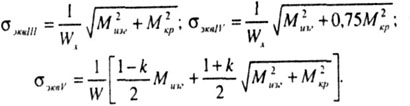| Практические расчеты на прочность по допускаемым напряжениям
при сложном напряженном состоянии ведутся, как правило, с использованием
формулы Мора. Для хрупких материалов хорошее соответствие с опытом дали
теории прочности, когда разрушение идет по схеме отрыва. Если же материал
обладает одинаковыми механическими характеристиками при растяжении и сжатии
(к = 1), то можно применить формулы гипотез наибольшего касательного напряжения
и энергии формоизменения. |
| |
|
При любом использовании материалов установите обратную ссылку на своем сайте.
<a href="http://lovi5.ru/" target=_blank>Рефераты, шпаргалки</a>