Многогранник, составленный из двух равных многоугольников
А1,
А2
... Аn
и В1,
В2,...
Вn,
расположенных в параллельных плоскостях и n параллелограммов, называется
призмой.
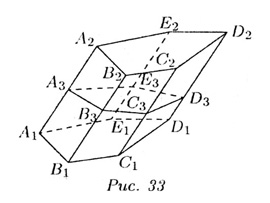
На рис. 33 соответствующие многоугольники являются пятиугольниками.
Площадью боковой поверхности призмы называется сумма площадей всех боковых
граней (параллелограммов). Перпендикулярным сечением призмы называется
многоугольник, который получается при пересечении плоскостей боковых граней
призмы плоскостью, перпендикулярной ее боковому ребру.
Теорема. Площадь боковой поверхности призмы
равна произведению периметра перпендикулярного сечения на боковое ребро.
Боковые ребра призмы перпендикулярны плоскости многоугольника А3,
В3,
С3,
D3,
E3.
Поэтому ребра сечения А3,
В3;
B3,
C3
и т.д. являются соответственно высотами боковых граней, т.е. параллелограммов
А1,
В1,
В2,
А2,
B1,
C1,
C2,
B2
и т. д., а тогда
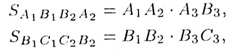
и т.д. Складывая эти равенства и учитывая, что А1,
A2
= B1,
B2
= ... , получаем
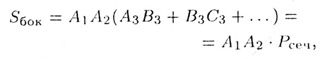
где Рсеч
— периметр перпендикулярного сечения.
Если призма прямая, Рсеч
равно периметру основания.
|
 При любом использовании материалов установите обратную ссылку на своем сайте.
При любом использовании материалов установите обратную ссылку на своем сайте.

 <a href="http://lovi5.ru/" target=_blank>Рефераты, шпаргалки</a>
<a href="http://lovi5.ru/" target=_blank>Рефераты, шпаргалки</a>